. clear . set more off
Set Working Directory
. cd "/Users/Sam/Desktop/Econ 645/Data/Wooldridge" /Users/Sam/Desktop/Econ 645/Data/Wooldridge
. use fertil3.dta, clear
Set Time Series
. tsset year
time variable: year, 1913 to 1984
delta: 1 unit
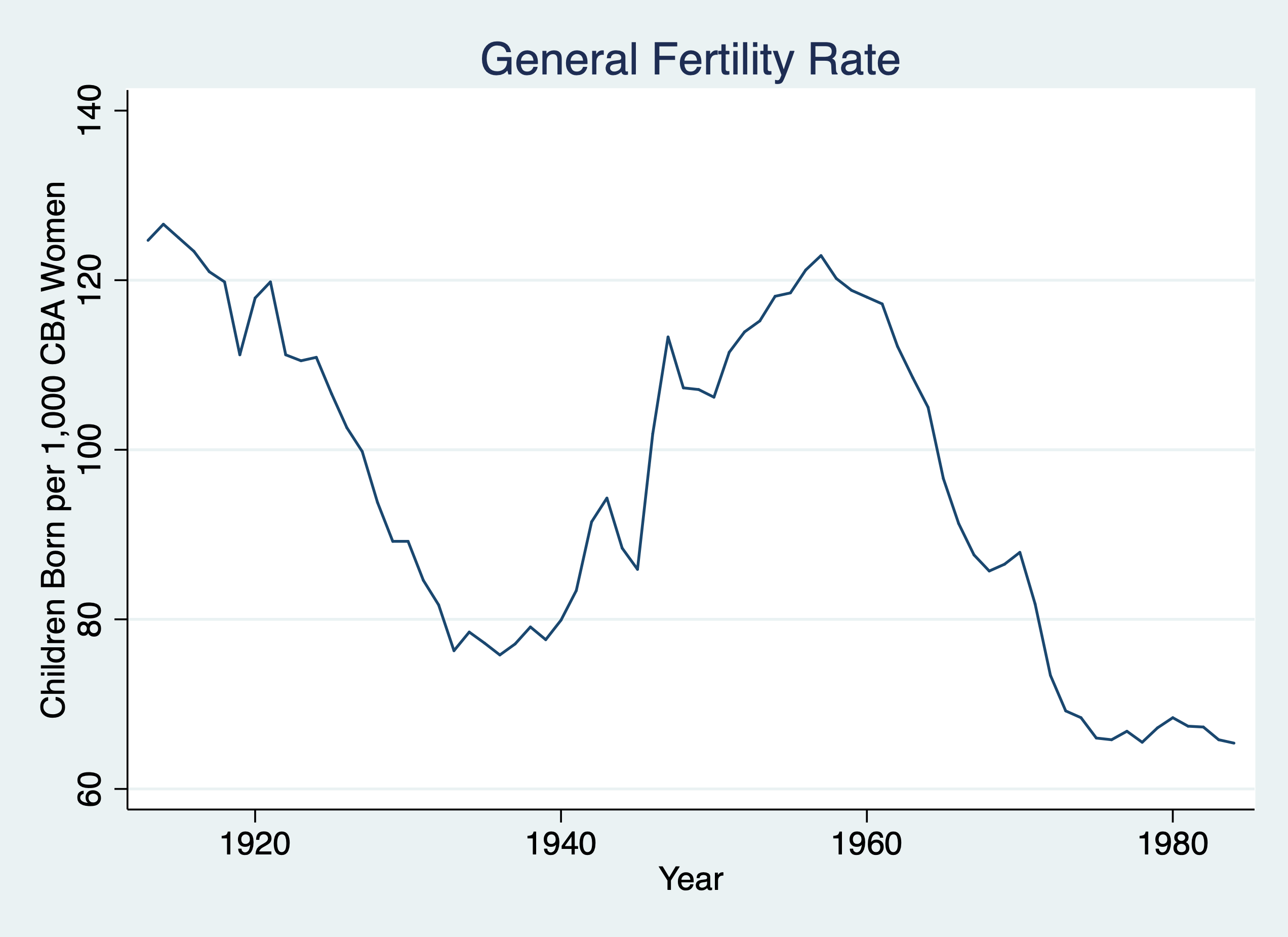
. twoway line gfr year, title("General Fertility Rate") ytitle("Children Born per 1,000 CBA Women") xtitle("Year")
. graph export "/Users/Sam/Desktop/Econ 645/Stata/week_11_i1.png", replace
(file /Users/Sam/Desktop/Econ 645/Stata/week_11_i1.png written in PNG format)

Estimate autocorrelation or estimate rho-hat
. reg gfr l.gfr
Source │ SS df MS Number of obs = 71
─────────────┼────────────────────────────────── F(1, 69) = 1413.53
Model │ 25734.824 1 25734.824 Prob > F = 0.0000
Residual │ 1256.21904 69 18.2060731 R-squared = 0.9535
─────────────┼────────────────────────────────── Adj R-squared = 0.9528
Total │ 26991.043 70 385.586329 Root MSE = 4.2669
─────────────┬────────────────────────────────────────────────────────────────
gfr │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
gfr │
L1. │ .9777202 .0260053 37.60 0.000 .925841 1.029599
│
_cons │ 1.304937 2.548821 0.51 0.610 -3.779822 6.389695
─────────────┴────────────────────────────────────────────────────────────────
Our result is rho-hat is 0.98, which is indicative of a unit root process. Under our TS assumptions our t statistics are invalid, but if we use a transformation using a first-difference process, we can relax those assumptions under the TSC assumptions. If our I(1) becomes I(0), then our TSC assumptions are potentially valid.
First Difference both dependent and independent
. reg d.gfr d.pe if year < 1985
Source │ SS df MS Number of obs = 71
─────────────┼────────────────────────────────── F(1, 69) = 2.26
Model │ 40.3237206 1 40.3237206 Prob > F = 0.1370
Residual │ 1229.25866 69 17.8153428 R-squared = 0.0318
─────────────┼────────────────────────────────── Adj R-squared = 0.0177
Total │ 1269.58238 70 18.1368911 Root MSE = 4.2208
─────────────┬────────────────────────────────────────────────────────────────
D.gfr │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
pe │
D1. │ -.0426776 .0283672 -1.50 0.137 -.0992686 .0139134
│
_cons │ -.7847796 .5020398 -1.56 0.123 -1.786322 .2167625
─────────────┴────────────────────────────────────────────────────────────────
Our result is that the real value of the personal exemption is associated with a 0.043 decrease in fertility or a 23 dollar increase in the real value of the personal exemption is associated with a 1 child per capita (1,000 CBA Women). This is a bit unexpected, but still insignificant. Let’s add some lags.
First differnce with more than 1 lag
. reg d.gfr d.pe d.pe_1 d.pe_2 if year < 1985
Source │ SS df MS Number of obs = 69
─────────────┼────────────────────────────────── F(3, 65) = 6.56
Model │ 293.259859 3 97.7532864 Prob > F = 0.0006
Residual │ 968.199959 65 14.895384 R-squared = 0.2325
─────────────┼────────────────────────────────── Adj R-squared = 0.1971
Total │ 1261.45982 68 18.5508797 Root MSE = 3.8595
─────────────┬────────────────────────────────────────────────────────────────
D.gfr │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
pe │
D1. │ -.0362021 .0267737 -1.35 0.181 -.089673 .0172687
│
pe_1 │
D1. │ -.0139706 .0275539 -0.51 0.614 -.0689997 .0410584
│
pe_2 │
D1. │ .1099896 .0268797 4.09 0.000 .0563071 .1636721
│
_cons │ -.9636787 .4677599 -2.06 0.043 -1.89786 -.0294976
─────────────┴────────────────────────────────────────────────────────────────
Our results show that increases in the current and prior period real value personal exemption is not statistically significant. However, a 1 dollar increase in the real value of personal exemption is associated two period prior is associated with an increase of .110 child per capita (or $9.1 increase is associated with an increase of 1 child per capita.
I(1) process with the presence of a linear trend
. use earns.dta, clear
Set Time Series
. tsset year, yearly
time variable: year, 1947 to 1987
delta: 1 year
We want to estimate the elasticity of hourly wage with respect to output per hour (or labor productivity). \[ ln(hrwage_t)=\beta_0 + \beta_1 ln(outphr_t) + \beta_2 t + u_t \]
We estimate the contemporaneous model
. reg lhrwage loutphr t
Source │ SS df MS Number of obs = 41
─────────────┼────────────────────────────────── F(2, 38) = 641.22
Model │ 1.04458064 2 .522290318 Prob > F = 0.0000
Residual │ .030951776 38 .00081452 R-squared = 0.9712
─────────────┼────────────────────────────────── Adj R-squared = 0.9697
Total │ 1.07553241 40 .02688831 Root MSE = .02854
─────────────┬────────────────────────────────────────────────────────────────
lhrwage │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
loutphr │ 1.639639 .0933471 17.56 0.000 1.450668 1.828611
t │ -.01823 .0017482 -10.43 0.000 -.021769 -.0146909
_cons │ -5.328454 .3744492 -14.23 0.000 -6.086487 -4.570421
─────────────┴────────────────────────────────────────────────────────────────
We estimate that the elasticity is very large, where a 1% increase in labor productivity (output per hour) is associated with a 1.64% increase in hourly wage. Let’s test for autocorrelation with accounting for the linear trend.
. reg lhrwage l.lhrwage t
Source │ SS df MS Number of obs = 40
─────────────┼────────────────────────────────── F(2, 37) = 1595.37
Model │ .921760671 2 .460880336 Prob > F = 0.0000
Residual │ .010688817 37 .000288887 R-squared = 0.9885
─────────────┼────────────────────────────────── Adj R-squared = 0.9879
Total │ .932449488 39 .023908961 Root MSE = .017
─────────────┬────────────────────────────────────────────────────────────────
lhrwage │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
lhrwage │
L1. │ .9842872 .0334331 29.44 0.000 .9165452 1.052029
│
t │ -.0009039 .0004732 -1.91 0.064 -.0018626 .0000548
_cons │ .0544169 .0413998 1.31 0.197 -.0294671 .1383008
─────────────┴────────────────────────────────────────────────────────────────
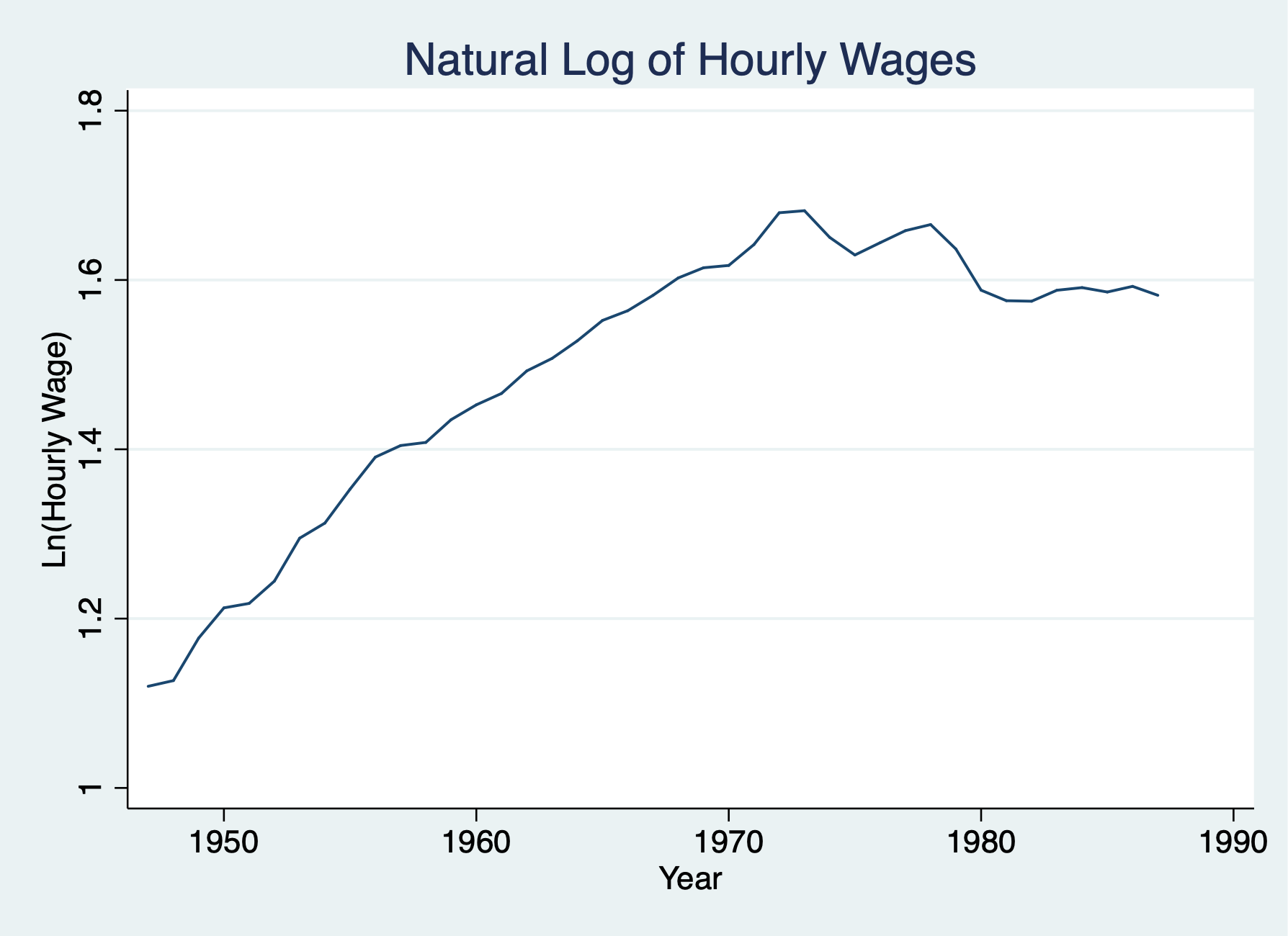
We have some evidence for a unit root process, so we’ll use the first-difference to transform the I(1) process into a I(0) process. We’ll no longer need the time trend
. twoway line lhrwage year, title("Natural Log of Hourly Wages") ytitle("Ln(Hourly Wage)") xtitle("Year")
. graph export "/Users/Sam/Desktop/Econ 645/Stata/week_11_hrwage1.png", replace
(file /Users/Sam/Desktop/Econ 645/Stata/week_11_hrwage1.png written in PNG format)
. twoway line d.lhrwage year, title("First-Difference in Ln(Hourly Wages)") ytitle("Delta Ln(Hourly Wage)") xtitle(
> "Year")
. graph export "/Users/Sam/Desktop/Econ 645/Stata/week_11_hrwage2.png", replace
(file /Users/Sam/Desktop/Econ 645/Stata/week_11_hrwage2.png written in PNG format)
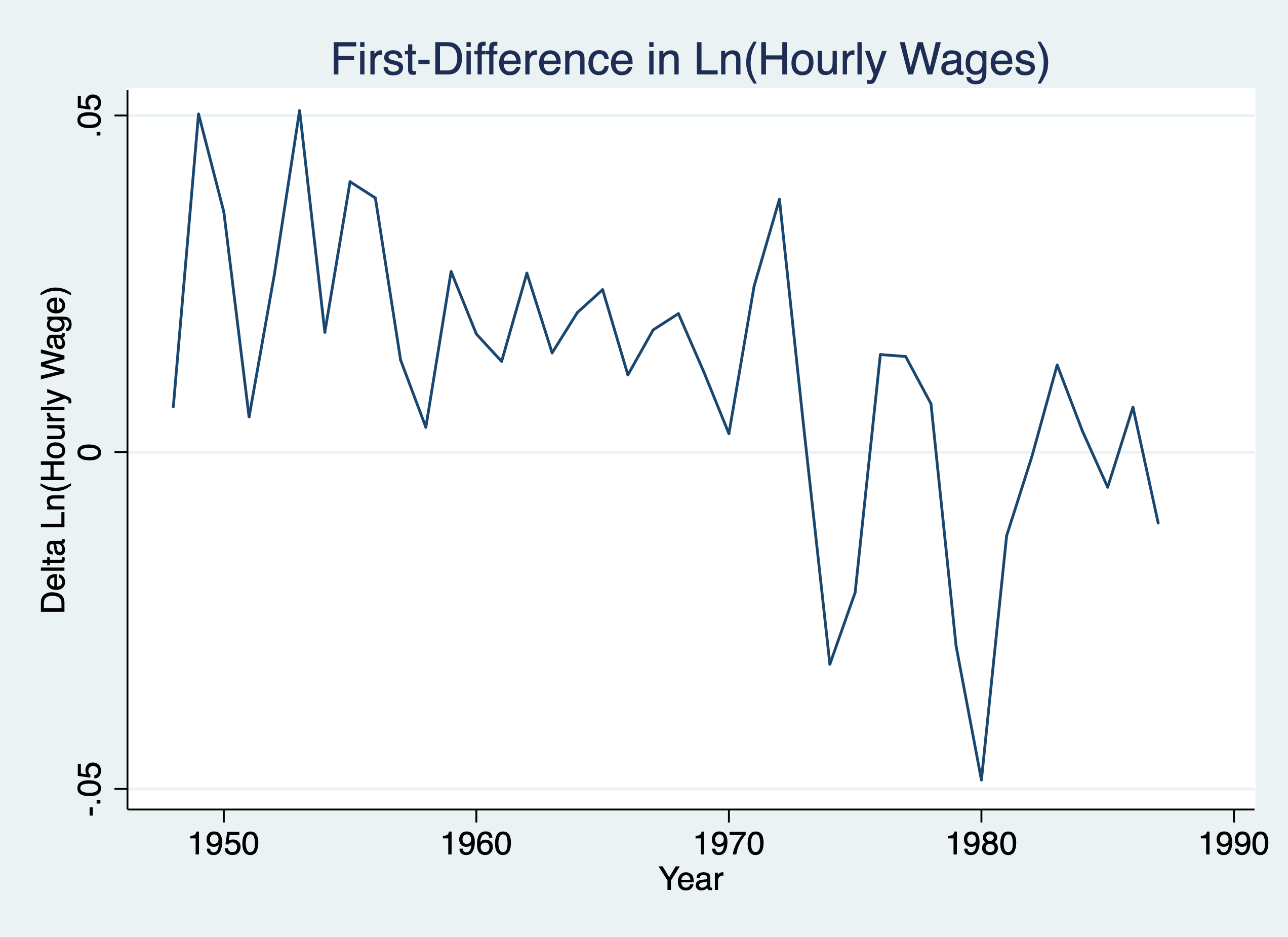
We’ll keep the trend based upon our prior graph
. reg d.lhrwage d.loutphr t
Source │ SS df MS Number of obs = 40
─────────────┼────────────────────────────────── F(2, 37) = 19.12
Model │ .008727211 2 .004363605 Prob > F = 0.0000
Residual │ .008445792 37 .000228265 R-squared = 0.5082
─────────────┼────────────────────────────────── Adj R-squared = 0.4816
Total │ .017173003 39 .000440333 Root MSE = .01511
─────────────┬────────────────────────────────────────────────────────────────
D.lhrwage │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
loutphr │
D1. │ .5511404 .1733698 3.18 0.003 .1998598 .9024209
│
t │ -.0007637 .0002321 -3.29 0.002 -.0012339 -.0002935
_cons │ .0176094 .0074784 2.35 0.024 .0024567 .0327622
─────────────┴────────────────────────────────────────────────────────────────
Our transformed model shows that a 1% increase in output per hour is associated with a .55% increase in hourly wage.
. use fertil3.dta
Set Time Series
. tsset year, yearly
time variable: year, 1913 to 1984
delta: 1 year
We’ll estimate a Finite Distributed Lag model for the first difference of general fertility onto the first difference of personal exemptions. If our model is dynamically complete, then no additional lags of gfr or pe are needed.
Our First-difference model with one lag of pe
. reg d.gfr d.pe d.pe_1 if year < 1985
Source │ SS df MS Number of obs = 70
─────────────┼────────────────────────────────── F(2, 67) = 1.20
Model │ 43.7985353 2 21.8992676 Prob > F = 0.3063
Residual │ 1218.19557 67 18.1820235 R-squared = 0.0347
─────────────┼────────────────────────────────── Adj R-squared = 0.0059
Total │ 1261.99411 69 18.2897697 Root MSE = 4.264
─────────────┬────────────────────────────────────────────────────────────────
D.gfr │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
pe │
D1. │ -.0456497 .0294689 -1.55 0.126 -.1044699 .0131704
│
pe_1 │
D1. │ .0134149 .0295326 0.45 0.651 -.0455324 .0723623
│
_cons │ -.8372962 .5117337 -1.64 0.106 -1.858721 .1841286
─────────────┴────────────────────────────────────────────────────────────────
Is this dynamically complete? Let’s add a second lag of pe
. reg d.gfr d.pe d.pe_1 d.pe_2 if year < 1985
Source │ SS df MS Number of obs = 69
─────────────┼────────────────────────────────── F(3, 65) = 6.56
Model │ 293.259859 3 97.7532864 Prob > F = 0.0006
Residual │ 968.199959 65 14.895384 R-squared = 0.2325
─────────────┼────────────────────────────────── Adj R-squared = 0.1971
Total │ 1261.45982 68 18.5508797 Root MSE = 3.8595
─────────────┬────────────────────────────────────────────────────────────────
D.gfr │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
pe │
D1. │ -.0362021 .0267737 -1.35 0.181 -.089673 .0172687
│
pe_1 │
D1. │ -.0139706 .0275539 -0.51 0.614 -.0689997 .0410584
│
pe_2 │
D1. │ .1099896 .0268797 4.09 0.000 .0563071 .1636721
│
_cons │ -.9636787 .4677599 -2.06 0.043 -1.89786 -.0294976
─────────────┴────────────────────────────────────────────────────────────────
Add lag of d.gfr and see it wasn’t dynamically complete
. reg d.gfr d.gfr_1 d.pe d.pe_1 d.pe_2 if year < 1985
Source │ SS df MS Number of obs = 69
─────────────┼────────────────────────────────── F(4, 64) = 7.46
Model │ 401.286162 4 100.32154 Prob > F = 0.0001
Residual │ 860.173657 64 13.4402134 R-squared = 0.3181
─────────────┼────────────────────────────────── Adj R-squared = 0.2755
Total │ 1261.45982 68 18.5508797 Root MSE = 3.6661
─────────────┬────────────────────────────────────────────────────────────────
D.gfr │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
gfr_1 │
D1. │ .3002422 .1059034 2.84 0.006 .0886758 .5118086
│
pe │
D1. │ -.0454721 .0256417 -1.77 0.081 -.0966972 .005753
│
pe_1 │
D1. │ .002064 .0267776 0.08 0.939 -.0514303 .0555584
│
pe_2 │
D1. │ .1051346 .0255904 4.11 0.000 .054012 .1562572
│
_cons │ -.7021594 .4537988 -1.55 0.127 -1.608727 .2044079
─────────────┴────────────────────────────────────────────────────────────────
We’ll use our t-test for serial correlation with strictly exogenous regressors under the assumption that our regressors are exogenous.
. use phillips.dta, clear
Set Time Series
. tsset year, yearly
time variable: year, 1948 to 2003
delta: 1 year
We estimated a static Phillips Curve and an augmented Phillips Curve last week. We’ll retest the models for serial correlation.
Test for serial correlation in Static Model Noticeable serial correlation
. reg inf unem if year < 1997
Source │ SS df MS Number of obs = 49
─────────────┼────────────────────────────────── F(1, 47) = 2.62
Model │ 25.6369575 1 25.6369575 Prob > F = 0.1125
Residual │ 460.61979 47 9.80042107 R-squared = 0.0527
─────────────┼────────────────────────────────── Adj R-squared = 0.0326
Total │ 486.256748 48 10.1303489 Root MSE = 3.1306
─────────────┬────────────────────────────────────────────────────────────────
inf │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
unem │ .4676257 .2891262 1.62 0.112 -.1140213 1.049273
_cons │ 1.42361 1.719015 0.83 0.412 -2.034602 4.881822
─────────────┴────────────────────────────────────────────────────────────────
Breusch-Godfrey Test
. estat bgodfrey
Breusch-Godfrey LM test for autocorrelation
─────────────┬─────────────────────────────────────────────────────────────
lags(p) │ chi2 df Prob > chi2
─────────────┼─────────────────────────────────────────────────────────────
1 │ 18.472 1 0.0000
─────────────┴─────────────────────────────────────────────────────────────
H0: no serial correlation
Simple AR(1) test
. predict u, resid
. reg u l.u, noconst
Source │ SS df MS Number of obs = 55
─────────────┼────────────────────────────────── F(1, 54) = 29.61
Model │ 161.010846 1 161.010846 Prob > F = 0.0000
Residual │ 293.652171 54 5.43800317 R-squared = 0.3541
─────────────┼────────────────────────────────── Adj R-squared = 0.3422
Total │ 454.663017 55 8.26660031 Root MSE = 2.332
─────────────┬────────────────────────────────────────────────────────────────
u │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
u │
L1. │ .5822453 .1070035 5.44 0.000 .3677161 .7967745
─────────────┴────────────────────────────────────────────────────────────────
Test for serial correlation in Augmented Serial correlation is removed with the first-difference in inflation
. reg d.inf unem if year < 1997
Source │ SS df MS Number of obs = 48
─────────────┼────────────────────────────────── F(1, 46) = 5.56
Model │ 33.3829996 1 33.3829996 Prob > F = 0.0227
Residual │ 276.305138 46 6.00663344 R-squared = 0.1078
─────────────┼────────────────────────────────── Adj R-squared = 0.0884
Total │ 309.688138 47 6.58910932 Root MSE = 2.4508
─────────────┬────────────────────────────────────────────────────────────────
D.inf │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
unem │ -.5425869 .2301559 -2.36 0.023 -1.005867 -.079307
_cons │ 3.030581 1.37681 2.20 0.033 .259206 5.801955
─────────────┴────────────────────────────────────────────────────────────────
. predict u2, resid
(1 missing value generated)
Breusch-Godfrey Test
. estat bgodfrey
Breusch-Godfrey LM test for autocorrelation
─────────────┬─────────────────────────────────────────────────────────────
lags(p) │ chi2 df Prob > chi2
─────────────┼─────────────────────────────────────────────────────────────
1 │ 0.062 1 0.8039
─────────────┴─────────────────────────────────────────────────────────────
H0: no serial correlation
Durban-Watson Test
. estat dwatson Durbin-Watson d-statistic( 2, 48) = 1.769648
\[ d_L = 1.503 \] \[ d_U = 1.585 \] \[ 1.769648 > 1.585 \] We fail to reject the null hypothesis.
AR(1) Test
. reg u2 l.u2, noconst
Source │ SS df MS Number of obs = 54
─────────────┼────────────────────────────────── F(1, 53) = 0.07
Model │ .267251656 1 .267251656 Prob > F = 0.7905
Residual │ 198.724905 53 3.74952651 R-squared = 0.0013
─────────────┼────────────────────────────────── Adj R-squared = -0.0175
Total │ 198.992157 54 3.68503994 Root MSE = 1.9364
─────────────┬────────────────────────────────────────────────────────────────
u2 │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
u2 │
L1. │ -.0308131 .1154154 -0.27 0.791 -.262307 .2006808
─────────────┴────────────────────────────────────────────────────────────────
Test change in error terms for FD assumption on serial correlation so that the differences in errors are not correlated.
. gen u2_1=l.u2 (2 missing values generated)
. reg d.u2 d.u2_1, noconst
Source │ SS df MS Number of obs = 53
─────────────┼────────────────────────────────── F(1, 52) = 2.01
Model │ 13.6239993 1 13.6239993 Prob > F = 0.1623
Residual │ 352.532902 52 6.77947888 R-squared = 0.0372
─────────────┼────────────────────────────────── Adj R-squared = 0.0187
Total │ 366.156901 53 6.90862078 Root MSE = 2.6037
─────────────┬────────────────────────────────────────────────────────────────
D.u2 │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
u2_1 │
D1. │ -.1661051 .1171734 -1.42 0.162 -.4012307 .0690204
─────────────┴────────────────────────────────────────────────────────────────
drop u u2
We fail to reject the null hypothesis that there is no serial correlation in the difference in error term.
Let’s add a lag in inflation to change our static model into a FDL model. We can also use the estat dwatson or dwstat
. reg inf l.inf unem if year < 1997
Source │ SS df MS Number of obs = 48
─────────────┼────────────────────────────────── F(2, 45) = 19.72
Model │ 219.518187 2 109.759094 Prob > F = 0.0000
Residual │ 250.471823 45 5.56604051 R-squared = 0.4671
─────────────┼────────────────────────────────── Adj R-squared = 0.4434
Total │ 469.99001 47 9.99978744 Root MSE = 2.3592
─────────────┬────────────────────────────────────────────────────────────────
inf │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
inf │
L1. │ .7278693 .1263167 5.76 0.000 .4734544 .9822841
│
unem │ -.2443814 .26124 -0.94 0.355 -.7705457 .2817829
_cons │ 2.43082 1.354276 1.79 0.079 -.2968325 5.158473
─────────────┴────────────────────────────────────────────────────────────────
. estat dwatson
Durbin-Watson d-statistic( 3, 48) = 1.477467
Or
. dwstat Durbin-Watson d-statistic( 3, 48) = 1.477467
First, let’s find our critical values:
https://www3.nd.edu/~wevans1/econ30331/Durbin_Watson_tables.pdf.
\[ DW(3,48)=1.48 \] and \[ d_L \approx 1.4 \] and \[ d_U \approx 1.67 \] so our DW test is
inconclusive. We’ll look at Durban-Watson and DW Tables again a bit
later.
Durban’s alternative statistic
. use prminwge, clear
Set Time Series
. tsset year
time variable: year, 1950 to 1987
delta: 1 unit
We’ll rerun our static model and regress the natural log of the employment-population ratio onto the natural log of the importance of minimum wage, the natural log of Puerto Rican Gross National Product, the natural log of US GNP, and a time trend.
. reg lprepop lmincov lprgnp lusgnp t if year < 1988
Source │ SS df MS Number of obs = 38
─────────────┼────────────────────────────────── F(4, 33) = 66.23
Model │ .284430187 4 .071107547 Prob > F = 0.0000
Residual │ .035428331 33 .001073586 R-squared = 0.8892
─────────────┼────────────────────────────────── Adj R-squared = 0.8758
Total │ .319858518 37 .008644825 Root MSE = .03277
─────────────┬────────────────────────────────────────────────────────────────
lprepop │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
lmincov │ -.2122612 .0401524 -5.29 0.000 -.2939518 -.1305706
lprgnp │ .2852386 .0804922 3.54 0.001 .121476 .4490012
lusgnp │ .4860463 .2219829 2.19 0.036 .0344188 .9376739
t │ -.0266633 .0046267 -5.76 0.000 -.0360765 -.0172502
_cons │ -6.663432 1.257831 -5.30 0.000 -9.222508 -4.104356
─────────────┴────────────────────────────────────────────────────────────────
. predict u, resid
Test Serial Correlation with Durbin’s alternative statistic, which is valid when we don’t have strictly exogenous regressors.
. reg u l.u lmincov lprgnp lusgnp t, noconst
Source │ SS df MS Number of obs = 37
─────────────┼────────────────────────────────── F(5, 32) = 1.92
Model │ .007182064 5 .001436413 Prob > F = 0.1191
Residual │ .023990478 32 .000749702 R-squared = 0.2304
─────────────┼────────────────────────────────── Adj R-squared = 0.1101
Total │ .031172542 37 .000842501 Root MSE = .02738
─────────────┬────────────────────────────────────────────────────────────────
u │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
u │
L1. │ .4757945 .1653074 2.88 0.007 .1390742 .8125147
│
lmincov │ .041425 .0346345 1.20 0.240 -.0291232 .1119732
lprgnp │ -.0522061 .0615544 -0.85 0.403 -.1775883 .0731762
lusgnp │ .0606233 .0644769 0.94 0.354 -.070712 .1919585
t │ -.0005264 .0015194 -0.35 0.731 -.0036213 .0025685
─────────────┴────────────────────────────────────────────────────────────────
We can see that we reject the null hypothesis, since our rho-hat is 0.48 and statistically significant.
. use barium.dta, clear
Set Time Series
. tsset t, monthly
time variable: t, 1960m2 to 1970m12
delta: 1 month
We’ll look at our barium chloride model again to see if ITC complaints affect behavior of foreign exporters. We may have higher order of serial correlation since we are using monthly data.
. reg lchnimp lchempi lgas lrtwex befile6 affile6 afdec6
Source │ SS df MS Number of obs = 131
─────────────┼────────────────────────────────── F(6, 124) = 9.06
Model │ 19.4051607 6 3.23419346 Prob > F = 0.0000
Residual │ 44.2470875 124 .356831351 R-squared = 0.3049
─────────────┼────────────────────────────────── Adj R-squared = 0.2712
Total │ 63.6522483 130 .489632679 Root MSE = .59735
─────────────┬────────────────────────────────────────────────────────────────
lchnimp │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
lchempi │ 3.117193 .4792021 6.50 0.000 2.168718 4.065668
lgas │ .1963504 .9066172 0.22 0.829 -1.598099 1.9908
lrtwex │ .9830183 .4001537 2.46 0.015 .1910022 1.775034
befile6 │ .0595739 .2609699 0.23 0.820 -.4569585 .5761064
affile6 │ -.0324064 .2642973 -0.12 0.903 -.5555249 .490712
afdec6 │ -.565245 .2858352 -1.98 0.050 -1.130993 .0005028
_cons │ -17.803 21.04537 -0.85 0.399 -59.45769 23.85169
─────────────┴────────────────────────────────────────────────────────────────
. predict u, resid
Test for p1=p2=p3=0 jointly with an F-test.
. reg u l.u l2.u l3.u lchempi lgas lrtwex befile6 affile6 afdec6, noconst
Source │ SS df MS Number of obs = 128
─────────────┼────────────────────────────────── F(9, 119) = 1.67
Model │ 4.8836741 9 .542630456 Prob > F = 0.1024
Residual │ 38.5511192 119 .323958985 R-squared = 0.1124
─────────────┼────────────────────────────────── Adj R-squared = 0.0453
Total │ 43.4347933 128 .339334323 Root MSE = .56917
─────────────┬────────────────────────────────────────────────────────────────
u │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
u │
L1. │ .215573 .0910635 2.37 0.020 .0352581 .3958878
L2. │ .1296804 .0917465 1.41 0.160 -.0519868 .3113477
L3. │ .1209405 .0906816 1.33 0.185 -.0586181 .3004992
│
lchempi │ -.105758 .4679356 -0.23 0.822 -1.032317 .8208012
lgas │ .0125667 .1187882 0.11 0.916 -.2226459 .2477792
lrtwex │ .0518992 .3452261 0.15 0.881 -.631683 .7354815
befile6 │ -.0730016 .249775 -0.29 0.771 -.567581 .4215779
affile6 │ -.122359 .2541453 -0.48 0.631 -.6255919 .380874
afdec6 │ -.0694522 .2737453 -0.25 0.800 -.6114953 .4725909
─────────────┴────────────────────────────────────────────────────────────────
Our reject the null hypothesis that all of the lags are equal to zero using an F-test.
. test l.u l2.u l3.u
( 1) L.u = 0
( 2) L2.u = 0
( 3) L3.u = 0
F( 3, 119) = 4.98
Prob > F = 0.0027
However, when we test our last two lags, they are jointly insignificant.
. test l2.u l3.u
( 1) L2.u = 0
( 2) L3.u = 0
F( 2, 119) = 2.42
Prob > F = 0.0930
. drop u
We have evidence of at least serial correlation to the order of one.
. use barium.dta, clear
Set Time Series
. tsset t, monthly
time variable: t, 1960m2 to 1970m12
delta: 1 month
. est clear
OLS
. eststo OLS: reg lchnimp lchempi lgas lrtwex befile6 affile6 afdec6
Source │ SS df MS Number of obs = 131
─────────────┼────────────────────────────────── F(6, 124) = 9.06
Model │ 19.4051607 6 3.23419346 Prob > F = 0.0000
Residual │ 44.2470875 124 .356831351 R-squared = 0.3049
─────────────┼────────────────────────────────── Adj R-squared = 0.2712
Total │ 63.6522483 130 .489632679 Root MSE = .59735
─────────────┬────────────────────────────────────────────────────────────────
lchnimp │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
lchempi │ 3.117193 .4792021 6.50 0.000 2.168718 4.065668
lgas │ .1963504 .9066172 0.22 0.829 -1.598099 1.9908
lrtwex │ .9830183 .4001537 2.46 0.015 .1910022 1.775034
befile6 │ .0595739 .2609699 0.23 0.820 -.4569585 .5761064
affile6 │ -.0324064 .2642973 -0.12 0.903 -.5555249 .490712
afdec6 │ -.565245 .2858352 -1.98 0.050 -1.130993 .0005028
_cons │ -17.803 21.04537 -0.85 0.399 -59.45769 23.85169
─────────────┴────────────────────────────────────────────────────────────────
Prais-Winsten
. eststo Prais: prais lchnimp lchempi lgas lrtwex befile6 affile6 afdec6
Iteration 0: rho = 0.0000
Iteration 1: rho = 0.2708
Iteration 2: rho = 0.2910
Iteration 3: rho = 0.2930
Iteration 4: rho = 0.2932
Iteration 5: rho = 0.2932
Iteration 6: rho = 0.2932
Iteration 7: rho = 0.2932
Prais-Winsten AR(1) regression -- iterated estimates
Source │ SS df MS Number of obs = 131
─────────────┼────────────────────────────────── F(6, 124) = 5.24
Model │ 10.3252323 6 1.72087205 Prob > F = 0.0001
Residual │ 40.7593886 124 .328704747 R-squared = 0.2021
─────────────┼────────────────────────────────── Adj R-squared = 0.1635
Total │ 51.0846209 130 .392958622 Root MSE = .57333
─────────────┬────────────────────────────────────────────────────────────────
lchnimp │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
lchempi │ 2.940949 .6328402 4.65 0.000 1.688381 4.193517
lgas │ 1.04638 .9773356 1.07 0.286 -.8880406 2.980801
lrtwex │ 1.132791 .5066578 2.24 0.027 .1299738 2.135609
befile6 │ -.0164787 .3193802 -0.05 0.959 -.6486216 .6156641
affile6 │ -.0331563 .3218101 -0.10 0.918 -.6701086 .603796
afdec6 │ -.5768122 .3419865 -1.69 0.094 -1.253699 .1000748
_cons │ -37.0777 22.7783 -1.63 0.106 -82.16235 8.006941
─────────────┼────────────────────────────────────────────────────────────────
rho │ .293217
─────────────┴────────────────────────────────────────────────────────────────
Durbin-Watson statistic (original) 1.458414
Durbin-Watson statistic (transformed) 2.087181
. predict u, resid
First, let’s find our critical values:
https://www3.nd.edu/~wevans1/econ30331/Durbin_Watson_tables.pdf.
For the OLS Estimator \[ DW(6,131) =
1.458414 \] For the Prasi-Winsten Estimator \[ DW(6,131) = 2.087181 \] and \[ d_L \approx 1.60 \] and \[ d_U \approx 1.81 \] We reject the null
hypothesis for the OLS estimator, but we fail to reject the null
hypothesis for the Prais-Winsten Estimator.
Our beta-hats in Prais-Winsten Estimator are similar to our OLS estimates, but our PW standard errors account for the serial correlation. Our OLS standard errors usually understate the actual sampling variation in the OLS estimators and should be treated with suspicion.
. esttab, mtitle se stat(N rho)
────────────────────────────────────────────
(1) (2)
OLS Prais
────────────────────────────────────────────
lchempi 3.117*** 2.941***
(0.479) (0.633)
lgas 0.196 1.046
(0.907) (0.977)
lrtwex 0.983* 1.133*
(0.400) (0.507)
befile6 0.0596 -0.0165
(0.261) (0.319)
affile6 -0.0324 -0.0332
(0.264) (0.322)
afdec6 -0.565 -0.577
(0.286) (0.342)
_cons -17.80 -37.08
(21.05) (22.78)
────────────────────────────────────────────
N 131 131
rho 0.293
────────────────────────────────────────────
Standard errors in parentheses
* p<0.05, ** p<0.01, *** p<0.001
There is serial correlation, but we account for it with the PW FGLS estimator
. reg u l.u lchnimp lchempi lgas lrtwex befile6 affile6 afdec6, noconst
Source │ SS df MS Number of obs = 130
─────────────┼────────────────────────────────── F(8, 122) = 640.05
Model │ 43.5543846 8 5.44429807 Prob > F = 0.0000
Residual │ 1.03773198 122 .008506 R-squared = 0.9767
─────────────┼────────────────────────────────── Adj R-squared = 0.9752
Total │ 44.5921166 130 .343016281 Root MSE = .09223
─────────────┬────────────────────────────────────────────────────────────────
u │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
u │
L1. │ .0309497 .0144099 2.15 0.034 .0024239 .0594755
│
lchnimp │ .9801231 .0143516 68.29 0.000 .9517128 1.008534
lchempi │ -2.98055 .0866866 -34.38 0.000 -3.152155 -2.808945
lgas │ .520767 .0203221 25.63 0.000 .4805374 .5609966
lrtwex │ -.7946765 .0568229 -13.99 0.000 -.9071631 -.6821898
befile6 │ -.0135381 .040266 -0.34 0.737 -.0932487 .0661725
affile6 │ .0355207 .0409758 0.87 0.388 -.045595 .1166365
afdec6 │ .5743468 .0450573 12.75 0.000 .4851514 .6635422
─────────────┴────────────────────────────────────────────────────────────────
. drop u
We’ll show another example comparing OLS and Prais-Winsten estimators. We’ll look at the static Phillips curve, which we know has serial correlation.
. use phillips.dta, clear
Set the Time Series
. tsset year
time variable: year, 1948 to 2003
delta: 1 unit
. est clear
OLS
. eststo OLS: reg inf unem if year < 1997
Source │ SS df MS Number of obs = 49
─────────────┼────────────────────────────────── F(1, 47) = 2.62
Model │ 25.6369575 1 25.6369575 Prob > F = 0.1125
Residual │ 460.61979 47 9.80042107 R-squared = 0.0527
─────────────┼────────────────────────────────── Adj R-squared = 0.0326
Total │ 486.256748 48 10.1303489 Root MSE = 3.1306
─────────────┬────────────────────────────────────────────────────────────────
inf │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
unem │ .4676257 .2891262 1.62 0.112 -.1140213 1.049273
_cons │ 1.42361 1.719015 0.83 0.412 -2.034602 4.881822
─────────────┴────────────────────────────────────────────────────────────────
Prais-Winsten
. eststo PW: prais inf unem if year < 1997
Iteration 0: rho = 0.0000
Iteration 1: rho = 0.5727
Iteration 2: rho = 0.7307
Iteration 3: rho = 0.7719
Iteration 4: rho = 0.7792
Iteration 5: rho = 0.7803
Iteration 6: rho = 0.7805
Iteration 7: rho = 0.7805
Iteration 8: rho = 0.7805
Iteration 9: rho = 0.7805
Prais-Winsten AR(1) regression -- iterated estimates
Source │ SS df MS Number of obs = 49
─────────────┼────────────────────────────────── F(1, 47) = 7.39
Model │ 37.9720609 1 37.9720609 Prob > F = 0.0092
Residual │ 241.618458 47 5.14081826 R-squared = 0.1358
─────────────┼────────────────────────────────── Adj R-squared = 0.1174
Total │ 279.590519 48 5.82480248 Root MSE = 2.2673
─────────────┬────────────────────────────────────────────────────────────────
inf │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
unem │ -.715659 .3134522 -2.28 0.027 -1.346244 -.0850744
_cons │ 8.295912 2.23143 3.72 0.001 3.806854 12.78497
─────────────┼────────────────────────────────────────────────────────────────
rho │ .7805446
─────────────┴────────────────────────────────────────────────────────────────
Durbin-Watson statistic (original) 0.802700
Durbin-Watson statistic (transformed) 1.909865
Prais-Winsten with Cochrane-Orcutt Transformation
. eststo PW_CO: prais inf unem if year < 1997, corc
Iteration 0: rho = 0.0000
Iteration 1: rho = 0.5727
Iteration 2: rho = 0.7160
Iteration 3: rho = 0.7611
Iteration 4: rho = 0.7715
Iteration 5: rho = 0.7735
Iteration 6: rho = 0.7740
Iteration 7: rho = 0.7740
Iteration 8: rho = 0.7740
Iteration 9: rho = 0.7741
Iteration 10: rho = 0.7741
Cochrane-Orcutt AR(1) regression -- iterated estimates
Source │ SS df MS Number of obs = 48
─────────────┼────────────────────────────────── F(1, 46) = 4.33
Model │ 22.4790685 1 22.4790685 Prob > F = 0.0430
Residual │ 238.604008 46 5.18704365 R-squared = 0.0861
─────────────┼────────────────────────────────── Adj R-squared = 0.0662
Total │ 261.083076 47 5.55495907 Root MSE = 2.2775
─────────────┬────────────────────────────────────────────────────────────────
inf │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
unem │ -.6653356 .3196035 -2.08 0.043 -1.308664 -.0220071
_cons │ 7.583458 2.38053 3.19 0.003 2.7917 12.37522
─────────────┼────────────────────────────────────────────────────────────────
rho │ .7740512
─────────────┴────────────────────────────────────────────────────────────────
Durbin-Watson statistic (original) 0.802700
Durbin-Watson statistic (transformed) 1.593634
FD
. eststo FD: reg d.inf d.unem if year < 1997
Source │ SS df MS Number of obs = 48
─────────────┼────────────────────────────────── F(1, 46) = 7.18
Model │ 41.8222052 1 41.8222052 Prob > F = 0.0102
Residual │ 267.865933 46 5.82317245 R-squared = 0.1350
─────────────┼────────────────────────────────── Adj R-squared = 0.1162
Total │ 309.688138 47 6.58910932 Root MSE = 2.4131
─────────────┬────────────────────────────────────────────────────────────────
D.inf │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
unem │
D1. │ -.8421708 .3142509 -2.68 0.010 -1.474725 -.2096165
│
_cons │ -.0781776 .3484621 -0.22 0.823 -.7795954 .6232401
─────────────┴────────────────────────────────────────────────────────────────
. esttab, mtitle se stat(N rho)
────────────────────────────────────────────────────────────────────────────
(1) (2) (3) (4)
OLS PW PW_CO FD
────────────────────────────────────────────────────────────────────────────
unem 0.468 -0.716* -0.665*
(0.289) (0.313) (0.320)
D.unem -0.842*
(0.314)
_cons 1.424 8.296*** 7.583** -0.0782
(1.719) (2.231) (2.381) (0.348)
────────────────────────────────────────────────────────────────────────────
N 49 49 48 48
rho 0.781 0.774
────────────────────────────────────────────────────────────────────────────
Standard errors in parentheses
* p<0.05, ** p<0.01, *** p<0.001
The OLS and PW estimators might give very different estimators if our assumptions of strict exogeneity and the a \[ Cov(x_(t+1)+x_(t-1),u_t)=0 \] fail. If that is the case then using OLS with a first-difference might be a better method. We can see that the difference is quite notable. With our OLS estimators, the tradeoff between inflation and employment is non-existent, but with the PW estimator our estimate of beta 1 is closer to our first-difference estimate of beta 1.
It is possible that there is no relationship with the static model, but the change in inflation and the change in unemployment are negatively related.
. use intdef.dta, clear
Set the Time Series
. tsset year
time variable: year, 1948 to 2003
delta: 1 unit
We’ll look at the relationship between interest rates from the 3-month T-bill rate (i3) and inflation rate (inf) and deficits as a percentage of GDP. Static Model
. reg i3 inf def if year < 2004
Source │ SS df MS Number of obs = 56
─────────────┼────────────────────────────────── F(2, 53) = 40.09
Model │ 272.420338 2 136.210169 Prob > F = 0.0000
Residual │ 180.054275 53 3.39725047 R-squared = 0.6021
─────────────┼────────────────────────────────── Adj R-squared = 0.5871
Total │ 452.474612 55 8.22681113 Root MSE = 1.8432
─────────────┬────────────────────────────────────────────────────────────────
i3 │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
inf │ .6058659 .0821348 7.38 0.000 .4411243 .7706074
def │ .5130579 .1183841 4.33 0.000 .2756095 .7505062
_cons │ 1.733266 .431967 4.01 0.000 .8668497 2.599682
─────────────┴────────────────────────────────────────────────────────────────
Get Durban-Watson Statistic
. dwstat Durbin-Watson d-statistic( 3, 56) = .7161527
Critical values d(3,56)=.716, at the 5% level dL = 1.452 dU=1.681 dwstat < dL so we reject the null hypothesis
. predict u, resid
. reg u l.u, noconst
Source │ SS df MS Number of obs = 55
─────────────┼────────────────────────────────── F(1, 54) = 32.83
Model │ 64.1034163 1 64.1034163 Prob > F = 0.0000
Residual │ 105.448636 54 1.95275252 R-squared = 0.3781
─────────────┼────────────────────────────────── Adj R-squared = 0.3666
Total │ 169.552053 55 3.08276459 Root MSE = 1.3974
─────────────┬────────────────────────────────────────────────────────────────
u │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
u │
L1. │ .6228816 .1087148 5.73 0.000 .4049216 .8408415
─────────────┴────────────────────────────────────────────────────────────────
. drop u
We find that we have notable serial correlation in the error term that is statistically significant. We’ll run a first-difference model next.
First differencing
. reg d.i3 d.inf d.def if year < 2004
Source │ SS df MS Number of obs = 55
─────────────┼────────────────────────────────── F(2, 52) = 5.57
Model │ 17.8058164 2 8.90290822 Prob > F = 0.0065
Residual │ 83.1753707 52 1.59952636 R-squared = 0.1763
─────────────┼────────────────────────────────── Adj R-squared = 0.1446
Total │ 100.981187 54 1.87002198 Root MSE = 1.2647
─────────────┬────────────────────────────────────────────────────────────────
D.i3 │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
inf │
D1. │ .1494892 .0921555 1.62 0.111 -.0354343 .3344127
│
def │
D1. │ -.1813151 .1476825 -1.23 0.225 -.4776618 .1150315
│
_cons │ .0417738 .1713874 0.24 0.808 -.3021401 .3856877
─────────────┴────────────────────────────────────────────────────────────────
. dwstat
Durbin-Watson d-statistic( 3, 55) = 1.796365
Critical values d(3,56)=1.796, at the 5% level dL = 1.452 dU=1.681 dwstat > dU so we fail to reject the null hypothesis
. predict u, resid
(1 missing value generated)
. reg u l.u, noconst
Source │ SS df MS Number of obs = 54
─────────────┼────────────────────────────────── F(1, 53) = 0.29
Model │ .427058269 1 .427058269 Prob > F = 0.5921
Residual │ 77.8807184 53 1.46944752 R-squared = 0.0055
─────────────┼────────────────────────────────── Adj R-squared = -0.0133
Total │ 78.3077766 54 1.45014401 Root MSE = 1.2122
─────────────┬────────────────────────────────────────────────────────────────
u │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
u │
L1. │ .0717246 .133046 0.54 0.592 -.1951318 .3385811
─────────────┴────────────────────────────────────────────────────────────────
The serial correlation is no longer a problem with our first difference model, since first differencing can transform a unit root process I(1) into a I(0) process.
with Heteroskedastic and Autocorrelation Consistent (HAC) standard errors.
. use prminwge.dta, clear
We’ll revisit our Puerto Rican examination of the impact of minimum wage importance We’ll use Heteroskedastic and Autocorrelation Consistent (HAC) standard errors, and we’ll compare OLS, OLS with HAC standard errors, and Prais-Winsten estimates We’ll allow a maximum lag order of autocorrelation up to 2 with the lag(2) option.
Set Time Series
. tsset year, yearly
time variable: year, 1950 to 1987
delta: 1 year
. est clear
OLS
. eststo OLS: reg lprepop lmincov lprgnp lusgnp t if year < 1988
Source │ SS df MS Number of obs = 38
─────────────┼────────────────────────────────── F(4, 33) = 66.23
Model │ .284430187 4 .071107547 Prob > F = 0.0000
Residual │ .035428331 33 .001073586 R-squared = 0.8892
─────────────┼────────────────────────────────── Adj R-squared = 0.8758
Total │ .319858518 37 .008644825 Root MSE = .03277
─────────────┬────────────────────────────────────────────────────────────────
lprepop │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
lmincov │ -.2122612 .0401524 -5.29 0.000 -.2939518 -.1305706
lprgnp │ .2852386 .0804922 3.54 0.001 .121476 .4490012
lusgnp │ .4860463 .2219829 2.19 0.036 .0344188 .9376739
t │ -.0266633 .0046267 -5.76 0.000 -.0360765 -.0172502
_cons │ -6.663432 1.257831 -5.30 0.000 -9.222508 -4.104356
─────────────┴────────────────────────────────────────────────────────────────
Newey with lag order 1
. eststo Newey1: newey lprepop lmincov lprgnp lusgnp t if year < 1988, lag(1)
Regression with Newey-West standard errors Number of obs = 38
maximum lag: 1 F( 4, 33) = 40.98
Prob > F = 0.0000
─────────────┬────────────────────────────────────────────────────────────────
│ Newey-West
lprepop │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
lmincov │ -.2122612 .0454552 -4.67 0.000 -.3047405 -.119782
lprgnp │ .2852386 .1001564 2.85 0.008 .081469 .4890083
lusgnp │ .4860463 .27194 1.79 0.083 -.0672197 1.039312
t │ -.0266633 .0054879 -4.86 0.000 -.0378285 -.0154981
_cons │ -6.663432 1.475245 -4.52 0.000 -9.664841 -3.662023
─────────────┴────────────────────────────────────────────────────────────────
Newey with lag order 2
. eststo Newey2: newey lprepop lmincov lprgnp lusgnp t if year < 1988, lag(2)
Regression with Newey-West standard errors Number of obs = 38
maximum lag: 2 F( 4, 33) = 37.84
Prob > F = 0.0000
─────────────┬────────────────────────────────────────────────────────────────
│ Newey-West
lprepop │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
lmincov │ -.2122612 .0457187 -4.64 0.000 -.3052766 -.1192459
lprgnp │ .2852386 .0996361 2.86 0.007 .0825275 .4879497
lusgnp │ .4860463 .2791124 1.74 0.091 -.0818122 1.053905
t │ -.0266633 .0057558 -4.63 0.000 -.0383736 -.014953
_cons │ -6.663432 1.536433 -4.34 0.000 -9.789329 -3.537535
─────────────┴────────────────────────────────────────────────────────────────
Prais-Winsten
. eststo PW: prais lprepop lmincov lprgnp lusgnp t if year < 1988
Iteration 0: rho = 0.0000
Iteration 1: rho = 0.4197
Iteration 2: rho = 0.5325
Iteration 3: rho = 0.5796
Iteration 4: rho = 0.5999
Iteration 5: rho = 0.6086
Iteration 6: rho = 0.6123
Iteration 7: rho = 0.6139
Iteration 8: rho = 0.6146
Iteration 9: rho = 0.6149
Iteration 10: rho = 0.6150
Iteration 11: rho = 0.6151
Iteration 12: rho = 0.6151
Iteration 13: rho = 0.6151
Iteration 14: rho = 0.6151
Iteration 15: rho = 0.6151
Iteration 16: rho = 0.6151
Prais-Winsten AR(1) regression -- iterated estimates
Source │ SS df MS Number of obs = 38
─────────────┼────────────────────────────────── F(4, 33) = 24.87
Model │ .080888012 4 .020222003 Prob > F = 0.0000
Residual │ .026835918 33 .00081321 R-squared = 0.7509
─────────────┼────────────────────────────────── Adj R-squared = 0.7207
Total │ .10772393 37 .002911458 Root MSE = .02852
─────────────┬────────────────────────────────────────────────────────────────
lprepop │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
lmincov │ -.1477111 .0458423 -3.22 0.003 -.2409779 -.0544443
lprgnp │ .2513828 .1164623 2.16 0.038 .0144384 .4883271
lusgnp │ .2557114 .2317498 1.10 0.278 -.2157872 .72721
t │ -.0205016 .005856 -3.50 0.001 -.0324158 -.0085875
_cons │ -4.652853 1.37647 -3.38 0.002 -7.453303 -1.852404
─────────────┼────────────────────────────────────────────────────────────────
rho │ .6151374
─────────────┴────────────────────────────────────────────────────────────────
Durbin-Watson statistic (original) 1.013709
Durbin-Watson statistic (transformed) 1.736277
With t-stats below estimated parameters
. esttab, mtitle scalars(F N)
────────────────────────────────────────────────────────────────────────────
(1) (2) (3) (4)
OLS Newey1 Newey2 PW
────────────────────────────────────────────────────────────────────────────
lmincov -0.212*** -0.212*** -0.212*** -0.148**
(-5.29) (-4.67) (-4.64) (-3.22)
lprgnp 0.285** 0.285** 0.285** 0.251*
(3.54) (2.85) (2.86) (2.16)
lusgnp 0.486* 0.486 0.486 0.256
(2.19) (1.79) (1.74) (1.10)
t -0.0267*** -0.0267*** -0.0267*** -0.0205**
(-5.76) (-4.86) (-4.63) (-3.50)
_cons -6.663*** -6.663*** -6.663*** -4.653**
(-5.30) (-4.52) (-4.34) (-3.38)
────────────────────────────────────────────────────────────────────────────
N 38 38 38 38
F 66.23 40.98 37.84 24.87
────────────────────────────────────────────────────────────────────────────
t statistics in parentheses
* p<0.05, ** p<0.01, *** p<0.001
With standard errors below the estimated parameters
. esttab, mtitle se scalars(F N)
────────────────────────────────────────────────────────────────────────────
(1) (2) (3) (4)
OLS Newey1 Newey2 PW
────────────────────────────────────────────────────────────────────────────
lmincov -0.212*** -0.212*** -0.212*** -0.148**
(0.0402) (0.0455) (0.0457) (0.0458)
lprgnp 0.285** 0.285** 0.285** 0.251*
(0.0805) (0.100) (0.0996) (0.116)
lusgnp 0.486* 0.486 0.486 0.256
(0.222) (0.272) (0.279) (0.232)
t -0.0267*** -0.0267*** -0.0267*** -0.0205**
(0.00463) (0.00549) (0.00576) (0.00586)
_cons -6.663*** -6.663*** -6.663*** -4.653**
(1.258) (1.475) (1.536) (1.376)
────────────────────────────────────────────────────────────────────────────
N 38 38 38 38
F 66.23 40.98 37.84 24.87
────────────────────────────────────────────────────────────────────────────
Standard errors in parentheses
* p<0.05, ** p<0.01, *** p<0.001
Notice how our t-stat have fallen and our standard errors have risen for our Newey1 and Newey2 compared to OLS. Also, notice how the Prais-Winsten beta-hat on minimum coverage is closer to 0, then OLS or OLS with HAC standard errors.
. use nyse.dta, clear
We’ll revisit our test of the Efficient Market Hypothesis with stock return data. We can test to see if our assumption of homoskedasticity is valid with our time series. This is a separate test than the test for serial correlation.
Set TIME Series
. tsset t, weekly
time variable: t, 1960w2 to 1973w16
delta: 1 week
OLS
. reg return l.return
Source │ SS df MS Number of obs = 689
─────────────┼────────────────────────────────── F(1, 687) = 2.40
Model │ 10.6866231 1 10.6866231 Prob > F = 0.1218
Residual │ 3059.73817 687 4.45376735 R-squared = 0.0035
─────────────┼────────────────────────────────── Adj R-squared = 0.0020
Total │ 3070.42479 688 4.46282673 Root MSE = 2.1104
─────────────┬────────────────────────────────────────────────────────────────
return │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
return │
L1. │ .0588984 .0380231 1.55 0.122 -.0157569 .1335538
│
_cons │ .179634 .0807419 2.22 0.026 .0211034 .3381646
─────────────┴────────────────────────────────────────────────────────────────
We’ll test heteroskedasticity with estat hettest
. estat hettest
Breusch-Pagan / Cook-Weisberg test for heteroskedasticity
Ho: Constant variance
Variables: fitted values of return
chi2(1) = 95.22
Prob > chi2 = 0.0000
We’ll manually calculate the Breusch-Pagan test
. predict u, residu
(2 missing values generated)
. gen u2=u^2
(2 missing values generated)
. reg u2 l.return
Source │ SS df MS Number of obs = 689
─────────────┼────────────────────────────────── F(1, 687) = 30.05
Model │ 3755.56877 1 3755.56877 Prob > F = 0.0000
Residual │ 85846.2961 687 124.958219 R-squared = 0.0419
─────────────┼────────────────────────────────── Adj R-squared = 0.0405
Total │ 89601.8649 688 130.235269 Root MSE = 11.178
─────────────┬────────────────────────────────────────────────────────────────
u2 │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
return │
L1. │ -1.104133 .2014029 -5.48 0.000 -1.499572 -.7086934
│
_cons │ 4.656501 .4276789 10.89 0.000 3.816786 5.496216
─────────────┴────────────────────────────────────────────────────────────────
Test for serial correlation
. reg u l.u, noconst
Source │ SS df MS Number of obs = 688
─────────────┼────────────────────────────────── F(1, 687) = 0.00
Model │ .00603936 1 .00603936 Prob > F = 0.9706
Residual │ 3059.08227 687 4.45281262 R-squared = 0.0000
─────────────┼────────────────────────────────── Adj R-squared = -0.0015
Total │ 3059.08831 688 4.44634929 Root MSE = 2.1102
─────────────┬────────────────────────────────────────────────────────────────
u │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
u │
L1. │ .001405 .0381496 0.04 0.971 -.0734987 .0763087
─────────────┴────────────────────────────────────────────────────────────────
We can see we reject the null hypothesis that the variance of the error term is constant, and heteroskedasticity is a problem.
We can use robust, or HAC standard errors, but since serial correlation is not a problem, then we don’t need newey estimator.
. reg return l.return, robust
Linear regression Number of obs = 689
F(1, 687) = 0.72
Prob > F = 0.3950
R-squared = 0.0035
Root MSE = 2.1104
─────────────┬────────────────────────────────────────────────────────────────
│ Robust
return │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
return │
L1. │ .0588984 .0692053 0.85 0.395 -.0769809 .1947777
│
_cons │ .179634 .0852916 2.11 0.036 .0121705 .3470975
─────────────┴────────────────────────────────────────────────────────────────
. newey return l.return, lag(1)
Regression with Newey-West standard errors Number of obs = 689
maximum lag: 1 F( 1, 687) = 0.74
Prob > F = 0.3895
─────────────┬────────────────────────────────────────────────────────────────
│ Newey-West
return │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
return │
L1. │ .0588984 .0684001 0.86 0.389 -.0754 .1931968
│
_cons │ .179634 .0855634 2.10 0.036 .0116369 .3476311
─────────────┴────────────────────────────────────────────────────────────────
Expected value does not depend on past returns, but the variance of the error term is not constant, and needs to be corrected.
. use phillips.dta, clear
We’ll use our Phillip’s Curve data to forecast unemployment one-step into the future
Set Time Series
. tsset year
time variable: year, 1948 to 2003
delta: 1 unit
tsline
. tsline inf . graph export "/Users/Sam/Desktop/Econ 645/Stata/week_11_inflation.png", replace (file /Users/Sam/Desktop/Econ 645/Stata/week_11_inflation.png written in PNG format)
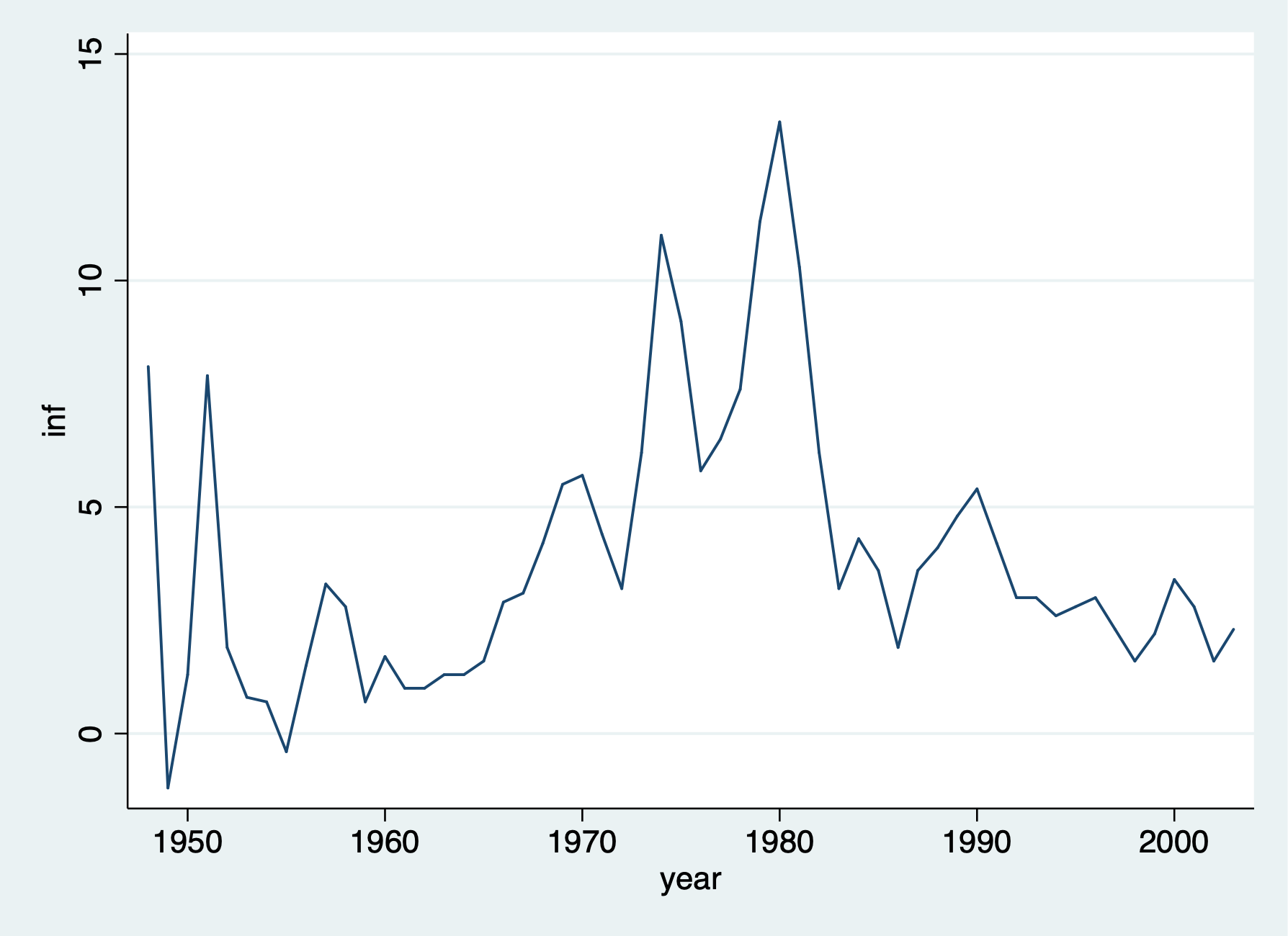
First we need to Generate training and test samples, so we’ll use the time series sequence until 1996 as our training data, and we’ll use 1997 to 2003 as our testing data.
. gen test = 0 . replace test = 1 if year >= 1997 (7 real changes made) . label define test1 0 "training sample" 1 "testing sample" . label values test test1We’ll use two models to forecast unemployment:
Compare models OLS AR(1)
. reg unem l.unem if test == 0
Source │ SS df MS Number of obs = 48
─────────────┼────────────────────────────────── F(1, 46) = 57.13
Model │ 62.8162728 1 62.8162728 Prob > F = 0.0000
Residual │ 50.5768515 46 1.09949677 R-squared = 0.5540
─────────────┼────────────────────────────────── Adj R-squared = 0.5443
Total │ 113.393124 47 2.41261967 Root MSE = 1.0486
─────────────┬────────────────────────────────────────────────────────────────
unem │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
unem │
L1. │ .7323538 .0968906 7.56 0.000 .537323 .9273845
│
_cons │ 1.571741 .5771181 2.72 0.009 .4100629 2.73342
─────────────┴────────────────────────────────────────────────────────────────
VAR - Add Lagged Inflation
. reg unem l.unem l.inf if test == 0
Source │ SS df MS Number of obs = 48
─────────────┼────────────────────────────────── F(2, 45) = 50.22
Model │ 78.3083336 2 39.1541668 Prob > F = 0.0000
Residual │ 35.0847907 45 .779662015 R-squared = 0.6906
─────────────┼────────────────────────────────── Adj R-squared = 0.6768
Total │ 113.393124 47 2.41261967 Root MSE = .88298
─────────────┬────────────────────────────────────────────────────────────────
unem │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
unem │
L1. │ .6470261 .0838056 7.72 0.000 .4782329 .8158192
│
inf │
L1. │ .1835766 .0411828 4.46 0.000 .1006302 .2665231
│
_cons │ 1.303797 .4896861 2.66 0.011 .3175188 2.290076
─────────────┴────────────────────────────────────────────────────────────────
One-step ahead we can use predict or forecast for AR(1)
. quietly reg unem l.unem if test == 0 . estimates store model1
We can get one-step ahead just using predict
. predict unem_est (option xb assumed; fitted values) (1 missing value generated)
Forecast - One-step-ahead forecast
. forecast create forecast1, replace (Forecast model forecast2 ended.) Forecast model forecast1 started. . forecast estimates model1 Added estimation results from regress. Forecast model forecast1 now contains 1 endogenous variable.
For a one-step ahead forecast, static is our key option otherwise it will not be a one-step ahead forecast.
. forecast solve, prefix(st_) begin(1997) end(2003) static Computing static forecasts for model forecast1. ─────────────────────────────────────────────── Starting period: 1997 Ending period: 2003 Forecast prefix: st_ 1997: ............. 1998: ............. 1999: .............. 2000: .............. 2001: .............. 2002: ............. 2003: ............ Forecast 1 variable spanning 7 periods. ───────────────────────────────────────
Dynamic model - We won’t use l.unem but l.dy_unem
. forecast solve, prefix(dy_) begin(1997) end(2003) Computing dynamic forecasts for model forecast1. ──────────────────────────────────────────────── Starting period: 1997 Ending period: 2003 Forecast prefix: dy_ 1997: ............. 1998: ............. 1999: ............ 2000: ............ 2001: ............ 2002: ............ 2003: ............ Forecast 1 variable spanning 7 periods. ───────────────────────────────────────
Graph Actual, One-Step-Ahead Model, and Dynamic Model
. twoway line unem year || line st_unem year, lpattern(dash) || line dy_unem year, lpattern(dot) . graph export "/Users/Sam/Desktop/Econ 645/Stata/week_11_static_v_dynamic.png", replace (file /Users/Sam/Desktop/Econ 645/Stata/week_11_static_v_dynamic.png written in PNG format)
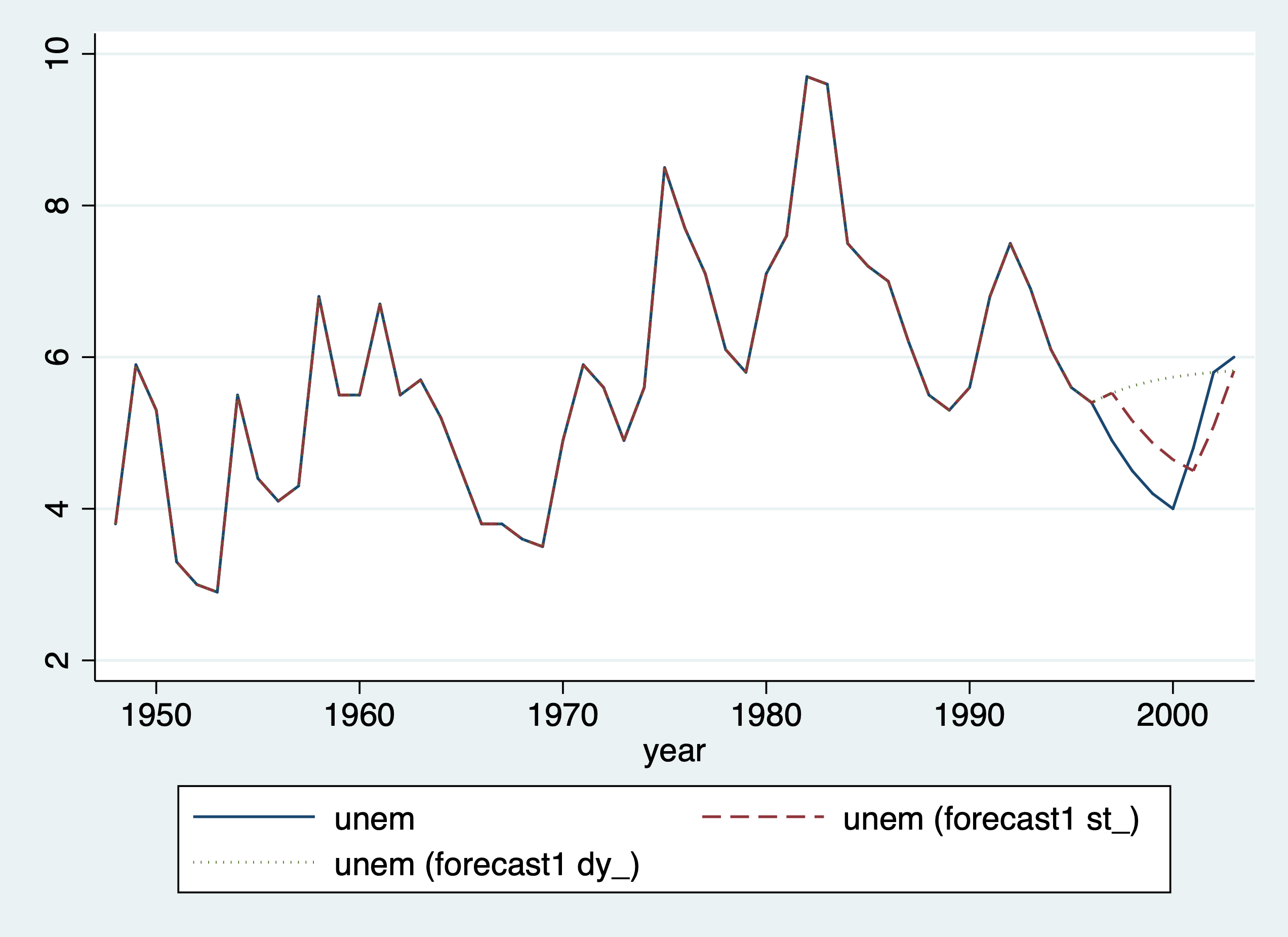
Calculate RMSE for Model 1
. gen e = unem - st_unem
. gen e2 = e^2
. sum e2 if test==1
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
e2 │ 7 .3319141 .1891047 .0326187 .5083123
. scalar esum= `r(sum)'/`r(N)'
. scalar model1_RMSE= esum^.5
. display model1_RMSE
.57611988
Calculate MAE for Model 1
. gen e_abs = abs(e) if test ==1
(49 missing values generated)
. sum e_abs if test==1
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
e_abs │ 7 .542014 .2109284 .1806064 .7129602
. scalar model1_MAE=`r(mean)'
. display model1_MAE
.54201399
One-step ahead we can use predict or forecast for VAR Model (lagged employment and lagged inflation) Get 1997 estimates
. quietly reg unem l.unem l.inf if year < 1997
Our predict command will produce the same results as forecast solve, static
. predict p2 (option xb assumed; fitted values) (1 missing value generated) . estimates store model2
Forecast for Model 2
. forecast create forecast2, replace (Forecast model forecast1 ended.) Forecast model forecast2 started. . forecast estimates model2 Added estimation results from regress. Forecast model forecast2 now contains 1 endogenous variable.
One-Step-Ahead Forecast of Model 2
. forecast solve, prefix(st2_) begin(1997) end(2003) static Computing static forecasts for model forecast2. ─────────────────────────────────────────────── Starting period: 1997 Ending period: 2003 Forecast prefix: st2_ 1997: ............ 1998: ........... 1999: ........... 2000: ............. 2001: .............. 2002: ............. 2003: .............. Forecast 1 variable spanning 7 periods. ───────────────────────────────────────
Dynamic Forecast of Model 2
. forecast solve, prefix(dy2_) begin(1997) end(2003) Computing dynamic forecasts for model forecast2. ──────────────────────────────────────────────── Starting period: 1997 Ending period: 2003 Forecast prefix: dy2_ 1997: ............ 1998: ............. 1999: ............. 2000: ............ 2001: ............. 2002: ............ 2003: ............. Forecast 1 variable spanning 7 periods. ───────────────────────────────────────
Calculate RMSE for Model 2
. drop e e2 e_abs
. gen e = unem - st2_unem
. gen e2 = e^2
. sum e2 if test==1
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
e2 │ 7 .2722276 .2459784 .080621 .7681881
. scalar esum2 = `r(sum)'/`r(N)'
. scalar model2_RMSE=esum2^.5
. display model2_RMSE
.52175434
Calculate MAE for Model 2
. gen e_abs = abs(e)
. sum e_abs if test==1
Variable │ Obs Mean Std. Dev. Min Max
─────────────┼─────────────────────────────────────────────────────────
e_abs │ 7 .4841946 .2099534 .2839384 .8764634
. scalar model2_MAE=`r(mean)'
Results
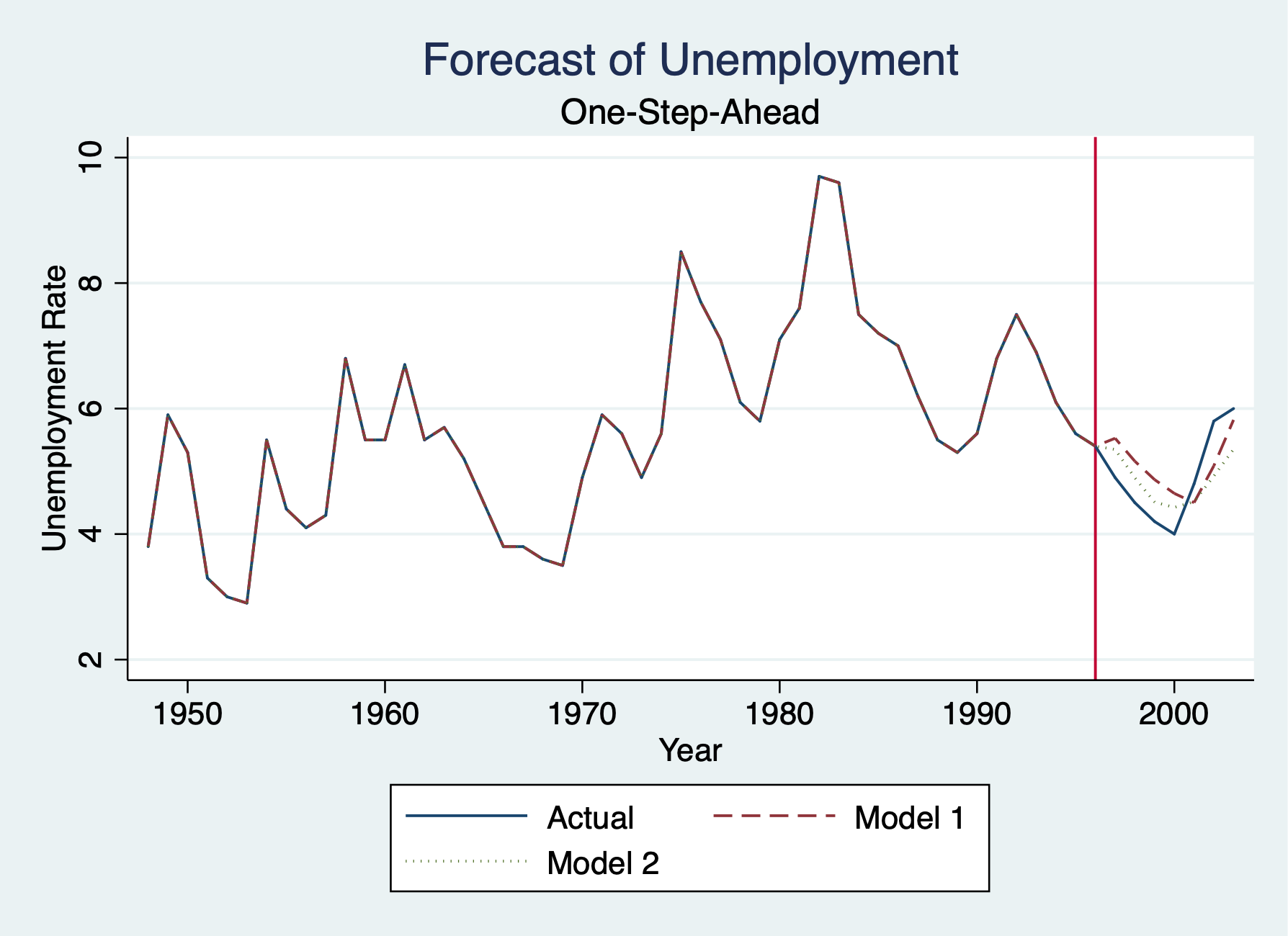
. display "Model 1: RMSE="model1_RMSE " and MAE="model1_MAE Model 1: RMSE=.57611988 and MAE=.54201399 . display "Model 2: RMSE="model2_RMSE " and MAE="model1_MAE Model 2: RMSE=.52175434 and MAE=.54201399 . display "Model 2 with lagged unemployment and lagged inflation has lower RMSE and MAE." Model 2 with lagged unemployment and lagged inflation has lower RMSE and MAE.
Forecasting Line
. twoway line unem year || line st_unem year, lpattern(dash) || line st2_unem year, lpattern(dot) ///
> title("Forecast of Unemployment") xtitle("Year") subtitle("One-Step-Ahead") ytitle("Unemployment Rate") xline(199
> 6) ///
> legend(order(1 "Actual" 2 "Model 1" 3 "Model 2"))
. graph export "/Users/Sam/Desktop/Econ 645/Stata/week_11_forecast.png", replace
(file /Users/Sam/Desktop/Econ 645/Stata/week_11_forecast.png written in PNG format)